SAT Strategies: Circles
- jsamuelbyrom
- Mar 14, 2023
- 2 min read
What do you expect when you think of circle questions? Most students tend to think of questions related to area and circumference-perhaps rotational motion, if they're taken Physics. And while those questions certainly can show up on the SAT, they're far from the most common: they tend to show up less than one time per test.
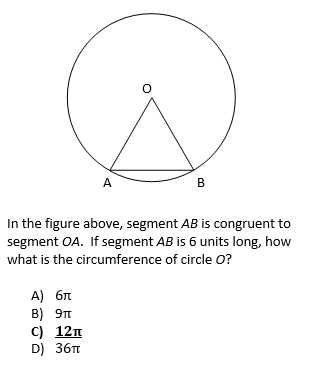
So then, what does show up on the test? Questions related to the graphs of circles.
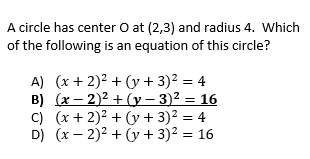
Test-takers tend to be much less prepared for this question type for a number of reasons. It's much more recent content; the graphs of circles first show up in Algebra 2. But a larger problem is has to deal with translation.
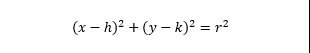
The graph of a circle with radius r and center (h, k) is shown above. Does anything about it stand out?
Astute students might notice that they're used to k being positive. For instance, Point-Slope Form for linear equations is usually written as:
y = m(x - h) + k
However, this is only appropriate when x and y are on the same side of the equation. A more precise understanding of translation can be gleaned by subtracting k from both sides:
(y - k) = m(x - h)
Here, we can see what really goes on with translation:
We've replaced x with (x - h) to shift it right by h.
We've replaced y with (y - k) to shift it up by k.
And these rules remain consistent for every equation you'll encounter! Circles? Same rules. Parabolas? Identical. Trigonometric graphs? Easy. Even in three dimensions, if you replace z with (z - l), you'll shift it in the positive z direction by l.
However, there's just one circle question that's even more difficult than those above-and it shows up on about 50% of SATs. If you're shooting for above a 700 in the Math section, see if you can figure it out!
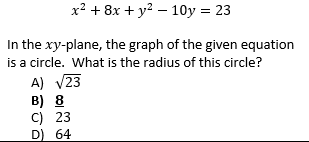
If you think you know why B is the correct choice, leave a comment below and see if you're right or not!




Comments